PRIZE PUZZLE FOR JANUARY 2008THE FOLDED SQUARE PROBLEM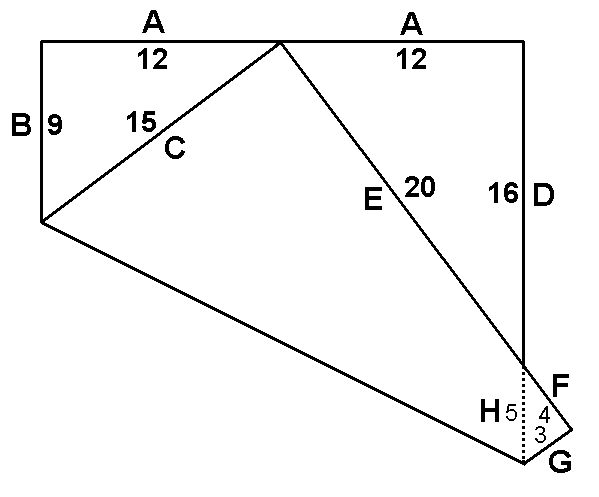
This diagram shows a square piece of paper folded so that one corner touches the centre of an opposite side. The letters A B C D E F G H are the dimensions of the various edge parts and all are integers (whole numbers) in whatever units you care to use. What is the smallest set of lengths for these eight dimensions? ANSWERSee diagram. The numbers can be found by fairly simple algebra; for example, B+C is the length of one side which is 2A. But because no absolute length is given you can't work out any individual lengths -- only ratios between them. So find the smallest common denominator for all the fractions and the numerators are then the lengths asked for. It is interesting that all three triangles are in the ratio 3:4:5.SOLVERSI received five correct answers. They were from Christopher Broughton (not in the draw), John Stafford, Richard Burkill (who won the draw), John Rackett and Clem Robertson (not in the draw by request). The winner received a £5 book token. |